

在漫长的数学史中小色哥萝莉网,欧几里得无疑是最伟大的念念想家之一。
他的著述《几何旨趣》,或称《元素》,不仅奠定了几何学的基础,还成为了通盘数学领域中最具影响力的经典作品之一。
手脚仅次于《圣经》的全国上翻译和传播最广的著述,《元素》对东谈主类的念念想和科学产生了深入影响。
欧几里得的伟大不单是在于他系统地冷落了几何学的基答应趣,更在于他创新性地将几何学的复杂性索要为一系列浅显的公理。
这种步调,不仅为几何学提供了一个逻辑明晰的框架,还鼓舞了通盘数学和科学领域的演绎推理的发展。
可是,尽管欧几里得的前四条公理被平凡经受,第五条公理,即闻明的“平行公设”,却激发了许无数学家的质疑和念念考。
01 欧几里得的第五公设与平行线的高深
第五公设的中枢在于平行线的行径。
它描摹了这么一个情况:要是两条直线被一条交叉线切割,何况交叉线一侧的内角之和小于180度,那么这两条直线在延永劫将会相交。
尽管这个假定看似浅显,但它的复杂性和不那么直不雅的性质让许无数学家感到不安。
相较于前四个不言自明的公理,第五公设似乎更像一个需要解说的定理,而不是基本真谛。
几千年来,无数的数学家试图从其他更浅显的公理中推导出第五公设。托勒密、阿尔哈曾和普罗克洛斯等数学家王人为之搜索枯肠,但未能告捷解说它是一个定理。
可是,19世纪初,一位名叫雅诺斯·博耶的匈牙利数学家冲破了这一局限。
02 雅诺斯·博耶与非欧几何的出身
博耶年青时便对第五公设的问题产生了浓厚的兴味,但他莫得像前东谈主那样试图解说它,而是冷落了一个立异性的目的:能够第五公设并不需要设置。这个念念路的冷落,径直导致了双曲几何和椭圆几何的出身。
 小色哥萝莉网
小色哥萝莉网
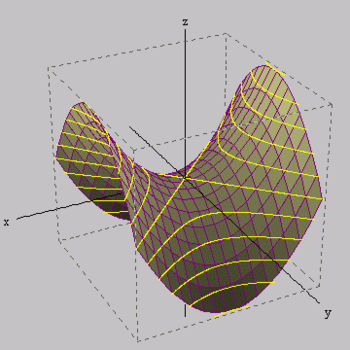
在双曲几何中,博耶和罗巴切夫斯基等数学家发现,通过一个给定点不错作出不啻一条与一条直线平行的线。
这与欧几里得几何中的单一平行线成见千差万别。在这种几何中,空间是负周折的,访佛于马鞍形的曲面。这种空间特点导致三角形的内角和老是小于180度。
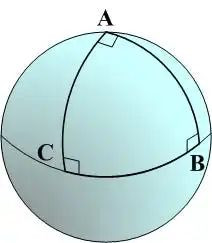
而在椭圆几何中,空间是正周折的,访佛于球面。
在这种几何中,扫数的直线最终王人会相交,也即是说根底不存在平行线。三角形的内角和老是大于180度,这不错通过在球面上绘画大圆形的三角形来不雅察。
这两种新几何学的发现,不仅转换了东谈主们对几何学的证实,还为描摹物理天地提供了新的器具。
尤其是在自后爱因斯坦的广义相对论中,椭圆几何被平凡哄骗,成为意会时空周折和引力的一部分。
03 时空的曲率与天地的神态
爱因斯坦的广义相对论依赖于黎曼几何,这是一种非欧几何。字据这一表面,空间和技巧并不是孤立存在的,它们共同组成了四维的时空,而大质地的物体会导致时空发生周折。
这种时空的曲率取代了牛顿的万有引力定律,解释了物体怎么沿着时空中的“直线”分解。
正如在橡胶膜上摈弃一个重球,小球沿着周折的橡胶膜轨迹分解雷同,行星和恒星在周折的时空中沿着弧线轨谈分解。
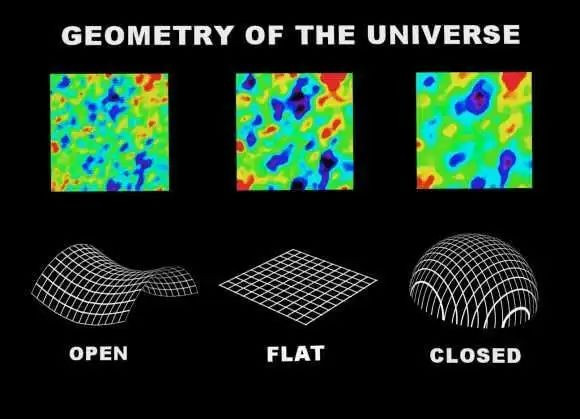
这种周折时空的几何结构,决定了天地的神态。科学家觉得,天地可能呈现三种几何阵势之一:
1、球面几何(正曲率):在这种几何中,天地是阻滞的,空间像球面雷同周折。平行线最终会相交,三角形的内角和大于180度。
2、这么的天地是有限的,但肥大界:就像你在地球上不错绕地球一圈又回到原点雷同。
3、平面几何(零曲率):这种天地的曲率为零,访佛于欧几里得几何。在这种几何中,平行线永不相交,三角形的内角和恰巧是180度。
天地是无穷的,并将以恒定的速率扩展。
4、双曲几何(负曲率):在双曲几何中,空间是负周折的,访佛于马鞍形。
平行线会发散,三角形的内角和小于180度。这种几何的天地是无穷的,何况会恒久加快膨大。
04 测量天地的神态:三角形的机密
要详情天地的神态,科学家们尝试测量天地中最大的三角形。这一目的基于这么一个事实:在非欧几何中,曲率的影响在大圭臬上会愈加权臣。
为了找到天地中最大的三角形,天体裁家转向了天地微波配景放射(CMB),这是大爆炸后留住的最陈旧的光。
通过测量CMB中的温度变化,科学家们能够分析这些变化点之间的角度。
普朗克探伤器的精密不雅测表示,这些角度真是完好合适平面几何的预期——三角形的内角和接近180度。
这一遵循让科学家们得出论断,天地是接近平坦的,尽管可能存在细微的偏差。
欧几里得在两千多年前冷落的几何公理,如今仍在匡助咱们解开天地的高深。发轫只是在古代几何学中的浅显假定,如今已演酿成一种测量时空和天地结构的器具。
数学不仅是一种描摹本质的谈话,它亦然咱们意会天地的瑕玷。通过数学,咱们能够冲破感知的极限,窥见无穷的真相,揭示天地最深层的机密。
追思:
今天,非欧几何学已成为好多科学领域的蹙迫器具,尤其是在物理学、天体裁和天地学中。它不仅让咱们对空间和技巧有了更深的意会,还鼓舞了拓扑学、代数几多么其他数学分支的发展。
这些数学器具为咱们描摹了一个比欧几里得几何更强大的全国小色哥萝莉网,并让咱们有智商探索和意会那些远超咱们直观的复杂成见。